Hex.*

LC497 - Random Pointin Non-Overlapping Rectangles

Posted on In
Leetcode: 121/2658 (52+56+13)

Description

You are given an array of non-overlapping axis-aligned rectangles rects where rects[i] = [ai, bi, xi, yi] indicates that (ai, bi) is the bottom-left corner point of the ith rectangle and (xi, yi) is the top-right corner point of the ith rectangle. Design an algorithm to pick a random integer point inside the space covered by one of the given rectangles. A point on the perimeter of a rectangle is included in the space covered by the rectangle.

Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.

Note that an integer point is a point that has integer coordinates.

Implement the Solution class:

Solution(int[][] rects) Initializes the object with the given rectangles rects.
int[] pick() Returns a random integer point [u, v] inside the space covered by one of the given rectangles.

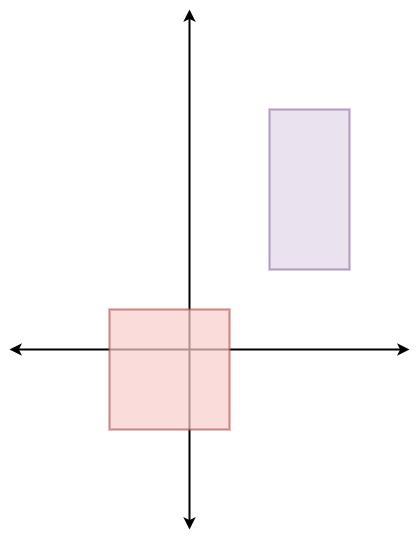
Example 1:

Input
[“Solution”, “pick”, “pick”, “pick”, “pick”, “pick”]
[[[[-2, -2, 1, 1], [2, 2, 4, 6]]], [], [], [], [], []]
Output
[null, [1, -2], [1, -1], [-1, -2], [-2, -2], [0, 0]]

Explanation
Solution solution = new Solution([[-2, -2, 1, 1], [2, 2, 4, 6]]);
solution.pick(); // return [1, -2]
solution.pick(); // return [1, -1]
solution.pick(); // return [-1, -2]
solution.pick(); // return [-2, -2]
solution.pick(); // return [0, 0]

Constraints:

1 <= rects.length <= 100
rects[i].length == 4
-109 <= ai < xi <= 109
-109 <= bi < yi <= 109
xi - ai <= 2000
yi - bi <= 2000
All the rectangles do not overlap.
At most 104 calls will be made to pick.

Solution

  • Calculate prefixes and arrays.
  • The last bit in the prefix sum array stores the total number of coordinate points at this time, so we choose a random number within this range.
  • See which interval the number is in the prefix and array, each interval represents a different rectangle. Since their weights are different, the subscript of each rectangle is selected according to its prefix and the number in the array. As shown in the figure below, the probability of selecting rectangle one is 9/37, the probability of selecting rectangle two is 12/37, and the probability of selecting square three is 16/37.
  • When a rectangle has been selected fairly after the above process is completed, we then randomly return a point in its rectangle according to the method in step disassembly
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:

    def __init__(self, rects: List[List[int]]):
        self.rects = rects
        self.presum = [0]
        for ai, bi, xi, yi in rects:
            self.presum.append(self.presum[-1]+(xi-ai+1) * (yi-bi+1))

    def pick(self) -> List[int]:
        val = random.randint(1, self.presum[-1])
        idx = bisect.bisect_left(self.presum, val) -1
        ai, bi, xi, yi = self.rects[idx]
        return [random.randint(ai, xi), random.randint(bi, yi)]

# Your Solution object will be instantiated and called as such:
# obj = Solution(rects)
# param_1 = obj.pick()