Hex.*

LC560 - Subarray Sum Equals K

Posted on In
Leetcode: 123/2658 (52+58+13)

Description

Given an array of integers nums and an integer k, return the total number of subarrays whose sum equals to k.

A subarray is a contiguous non-empty sequence of elements within an array.

Example 1:

Input: nums = [1,1,1], k = 2
Output: 2
Example 2:

Input: nums = [1,2,3], k = 3
Output: 2

Constraints:

1 <= nums.length <= 2 * 104
-1000 <= nums[i] <= 1000
-107 <= k <= 107

Solution

  • Each element corresponds to a “prefix sum”
  • Traverse the array to find the historical prefix sum of “subtract it == k” in the map based on the current “prefix sum”
  • The difference between the current “prefix sum” and the historical prefix sum is a sub-array. If the historical prefix sum occurs c times, it means that the current item finds c sub-arrays and the sum is equal to k.
  • During the traversal process, c is continuously added to count, and finally returns count
1
2
3
4
5
6
7
8
9
10
11
12
13
# O(n^2) time | O(n) space-- Time Out Exceed
class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        presum = [0]
        for i, v in enumerate(nums):
            presum.append(presum[-1] + v)

        cnt = 0
        for i in range(len(presum)):
            for j in range(i+1, len(presum)):
                if presum[j] - presum[i] == k:
                    cnt+=1
        return cnt

Prefix Sum + Hash Table

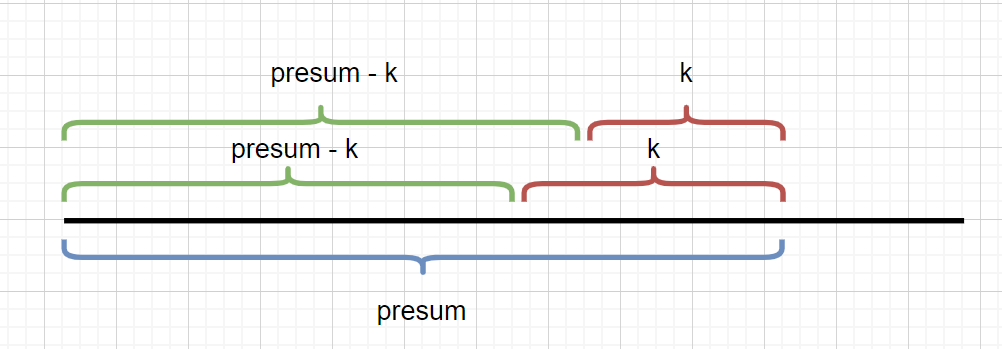
We need to find the interval that satisfies the sum K. At this time, presum is known, and k is also known. We only need to find the number of presum - k intervals to get the number of k intervals.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# O(n) time | O(n) space
class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        presum = {0:1}
        cur = 0
        res = 0
        for i in nums:
            cur += i
            if cur - k in presum:
                res += presum[cur-k]

            if cur not in presum:
                presum[cur] = 1
            else:
                presum[cur] += 1
            
        return res