Hex.*

LC508 - Most Frequent SubtreeSum

Posted on In
Leetcode: 134/2658 (56+64+14)

Description

Given the root of a binary tree, return the most frequent subtree sum. If there is a tie, return all the values with the highest frequency in any order.
The subtree sum of a node is defined as the sum of all the node values formed by the subtree rooted at that node (including the node itself).

Example 1:

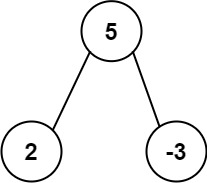
Input: root = [5,2,-3]
Output: [2,-3,4]

Example 2:

Input: root = [5,2,-5]
Output: [2]

Constraints:
The number of nodes in the tree is in the range [1, 104].
-105 <= Node.val <= 105

Solution

The case means:

example 1: Input [5,2,-3], then the subtree sum is 5 + 2 - 3 = 4, subtree 2, subtree -3, so the number of occurrences of each is equal, and directly returns [2,- 3,4].

example 2: Input [5,2,-5], subtree 2, subtree-5, and subtree and 5 + 2 - 5 = 2, so the maximum number of occurrences is 2.

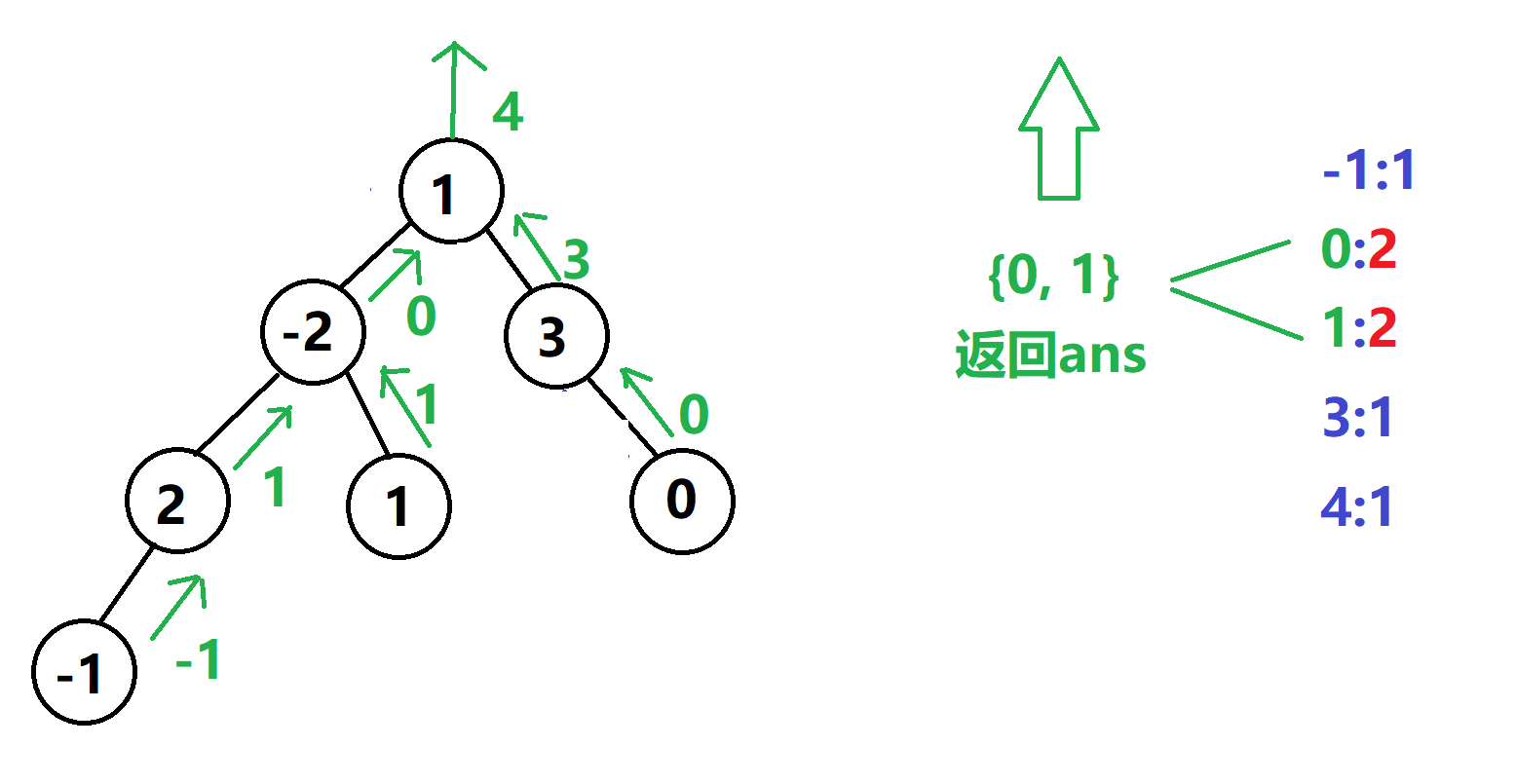
  • Traverse Order: left -> right -> root.
  • The value of the update root is the sum of the left subtree and right subtree.
  • Store the number of occurrences of the sum in the dictionary
  • Use max() to find the number with the largest value in the dictionary, traverse the dictionary, store the value and the key of the largest number in ans, and return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

# O(n) time | O(n) space
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findFrequentTreeSum(self, root: TreeNode) -> List[int]:
        summ = {}
        ans = []

        self.dfs(root, summ)
        maxVal = max(summ.values())
        for key, val in summ.items():
            if val == maxVal:
                ans.append(key)
        return ans
        
    
    def dfs(self, root, summ):
        if root is None:
            return 
        self.dfs(root.left, summ)
        self.dfs(root.right, summ)

        if root.left:
            root.val += root.left.val
        if root.right:
            root.val += root.right.val
        if root.val not in summ:
            summ[root.val] =1
        else:
            summ[root.val]+=1