Hex.*

LC1162 - as Far From Land as Possible

Posted on In
Leetcode: 150/2658 (59+72+19)

Description

Given an n x n grid containing only values 0 and 1, where 0 represents water and 1 represents land, find a water cell such that its distance to the nearest land cell is maximized, and return the distance. If no land or water exists in the grid, return -1.
The distance used in this problem is the Manhattan distance: the distance between two cells (x0, y0) and (x1, y1) is |x0 - x1| + |y0 - y1|.

Example 1:

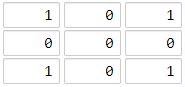
Input: grid = [[1,0,1],[0,0,0],[1,0,1]]
Output: 2
Explanation: The cell (1, 1) is as far as possible from all the land with distance 2.

Example 2:

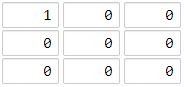
Input: grid = [[1,0,0],[0,0,0],[0,0,0]]
Output: 4
Explanation: The cell (2, 2) is as far as possible from all the land with distance 4.

Constraints:
n == grid.length
n == grid[i].length
1 <= n <= 100
grid[i][j] is 0 or 1

Solution

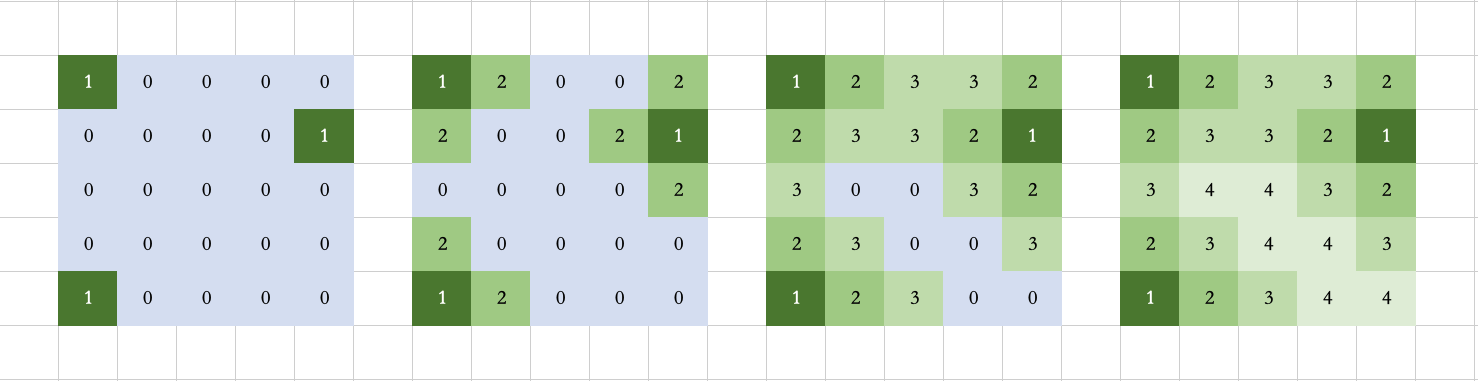
This question can be done using the multi-source breadth-first search method I did yesterday

  1. First save the coordinates of the current land to the queue
  2. Then start the breadth-first search through these coordinates
  3. In the process of traversing, the distance should be reduced by 1

Note: because if it is all land or all water, it returns -1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# O(n^2) time | O(n^2) space 
from collections import deque

class Solution:
    def maxDistance(self, grid: List[List[int]]) -> int:
        n = len(grid)
        queue = deque([])
        for r in range(n):
            for c in range(n):
                if grid[r][c]:
                    queue.append((r,c))
        maxi = -1

        while queue:
            row, col = queue.popleft()
            for dx, dy in [(0,1),(0,-1),(1,0),(-1,0)]:
                nx, ny = row+dx, col+dy
                if 0<= nx < n and 0<=ny<n and grid[nx][ny] == 0:
                    grid[nx][ny] = grid[row][col] +1
                    queue.append((nx,ny))
                    if grid[nx][ny] > maxi:
                        maxi = grid[nx][ny] -1
        return maxi