Hex.*

LC1217 - Minimum Cost to Move Chips to the Same Position

Posted on In
Leetcode: 152/2658 (59+74+19)

Description

We have n chips, where the position of the ith chip is position[i].
We need to move all the chips to the same position. In one step, we can change the position of the ith chip from position[i] to:
position[i] + 2 or position[i] - 2 with cost = 0.
position[i] + 1 or position[i] - 1 with cost = 1.
Return the minimum cost needed to move all the chips to the same position.

Example 1:

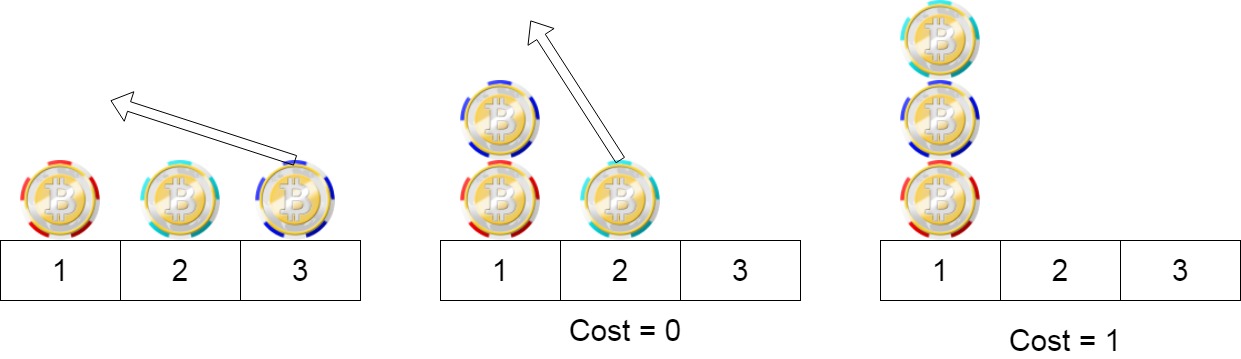
Input: position = [1,2,3]
Output: 1
Explanation: First step: Move the chip at position 3 to position 1 with cost = 0.
Second step: Move the chip at position 2 to position 1 with cost = 1.
Total cost is 1.

Example 2:

Input: position = [2,2,2,3,3]
Output: 2
Explanation: We can move the two chips at position 3 to position 2. Each move has cost = 1. The total cost = 2.

Example 3:
Input: position = [1,1000000000]
Output: 1

Constraints:
1 <= position.length <= 100
1 <= position[i] <= 10^9

Solution

This is a greedy problem, you need to realize that the cost is not related to the specific location, only the parity of the location
The cost for each chip move is:

  • Move two locations with 0 cost
  • Moving one position has a cost of 1 easy to get: the cost of moving from odd-numbered bits to odd-numbered bits is always 0, and the cost of moving from even-numbered bits to even-numbered bits is always 0.

Method1

Use a dictionary to store the number of times the coin appears at each position, then iterate over the dictionary and sum the parity separately.
Returns the smaller of two odd and even numbers.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# O(n) time | O(n) space
class Solution:
    def minCostToMoveChips(self, position: List[int]) -> int:
        coins = {}
        for coin in position:
            if coin not in coins:
                coins[coin] = 1
            else:
                coins[coin] +=1
        
        odd, even = 0, 0
        for key, val in coins.items():
            if key % 2 == 0:
                even += val
            else:
                odd += val
        return min(even, odd)

Optimize space complexity

Determine the parity directly when traversing the input, and then add 1 to the result of the parity

1
2
3
4
5
6
7
8
9
10
11
# O(n) time | O(1) space

class Solution:
    def minCostToMoveChips(self, position: List[int]) -> int:        
        odd, even = 0, 0
        for val in position:
            if val % 2 == 0:
                even += 1
            else:
                odd += 1
        return min(even, odd)

Pythonic Version

Determine if it is odd:

  1. cur % 2 == 1
  2. cur & 1

&

It is a bitwise AND operation. In bitwise binary operations, the two numbers in their binary form are processed by their corresponding bits. So 1 is only one bit. It will be compared to last bit of a number. So a&1 will return 1 if last bit of 1 is 1 and zero otherwise.

:=

starting in Python 3.8, := is actually a valid operator that allows for assignment of variables within expressions

1
2
3
class Solution:
    def minCostToMoveChips(self, position: List[int]) -> int:
        return min(odds := sum(p & 1 for p in position), len(position) - odds)