Hex.*

LC1260 - Shift 2D Grid

Posted on In
Datastructure and Algorithm: DAY 50. Leetcode: 204/2710

Description

Given a 2D grid of size m x n and an integer k. You need to shift the grid k times.
In one shift operation:
Element at grid[i][j] moves to grid[i][j + 1].
Element at grid[i][n - 1] moves to grid[i + 1][0].
Element at grid[m - 1][n - 1] moves to grid[0][0].
Return the 2D grid after applying shift operation k times.

Example 1:

1
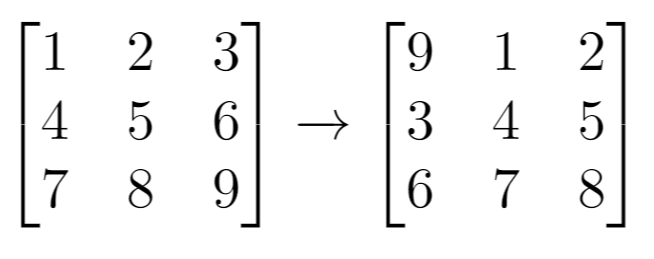
2
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
Output: [[9,1,2],[3,4,5],[6,7,8]]

Example 2:

1
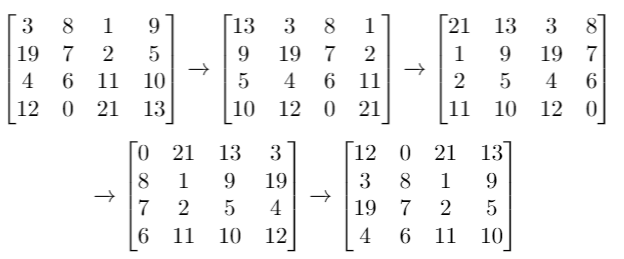
2
Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

Example 3:

1
2
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
Output: [[1,2,3],[4,5,6],[7,8,9]]

Constraints:
m == grid.length
n == grid[i].length
1 <= m <= 50
1 <= n <= 50
-1000 <= grid[i][j] <= 1000
0 <= k <= 100

Solutions

  • Flatten to a one-dimensional list with k step: vector
  • Convert to two-dimensional according to the number of rows and columns: metrix
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    # O(nm) time | O(nm) space
    class Solution:
        def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
            m, n = len(grid), len(grid[0])
            vector = [0] * m*n
            cur_idx = 0
            for r in range(m):
                for c in range(n):
                    idx = (cur_idx+k)% (m*n)
                    vector[idx] = grid[r][c]
                    cur_idx+=1

            idx = 0
            ans = []
            for r in range(m):
                level = []
                for c in range(n):
                    level.append(vector[idx])
                    idx+=1
                ans.append(level)
            return ans

Optimize space complexity

1
2
3
4
5
6
7
8
9
10
11
12
13
# O(nm) time | O(1) space

class Solution:
    def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
        m, n = len(grid), len(grid[0])
        matrix = [[0] * n for _ in range(m)]
        cur_idx = 0
        for r in range(m):
            for c in range(n):
                idx = (cur_idx+k)% (m*n)
                matrix[idx//n][idx%n] = grid[r][c]
                cur_idx+=1
        return matrix