Hex.*

LC851 - Loud and Rich

Posted on In
Datastructure and Algorithm: DAY 51. Leetcode: 207/2710

Description

There is a group of n people labeled from 0 to n - 1 where each person has a different amount of money and a different level of quietness.
You are given an array richer where richer[i] = [ai, bi] indicates that ai has more money than bi and an integer array quiet where quiet[i] is the quietness of the ith person. All the given data in richer are logically correct (i.e., the data will not lead you to a situation where x is richer than y and y is richer than x at the same time).
Return an integer array answer where answer[x] = y if y is the least quiet person (that is, the person y with the smallest value of quiet[y]) among all people who definitely have equal to or more money than the person x.

Example 1:

1
2
3
4
5
6
7
8
9
Input: richer = [[1,0],[2,1],[3,1],[3,7],[4,3],[5,3],[6,3]], quiet = [3,2,5,4,6,1,7,0]
Output: [5,5,2,5,4,5,6,7]
Explanation: 
answer[0] = 5.
Person 5 has more money than 3, which has more money than 1, which has more money than 0.
The only person who is quieter (has lower quiet[x]) is person 7, but it is not clear if they have more money than person 0.
answer[7] = 7.
Among all people that definitely have equal to or more money than person 7 (which could be persons 3, 4, 5, 6, or 7), the person who is the quietest (has lower quiet[x]) is person 7.
The other answers can be filled out with similar reasoning.

Example 2:

1
2
Input: richer = [], quiet = [0]
Output: [0]

Constraints:
n == quiet.length
1 <= n <= 500
0 <= quiet[i] < n
All the values of quiet are unique.
0 <= richer.length <= n * (n - 1) / 2
0 <= ai, bi < n
ai != bi
All the pairs of richer are unique.
The observations in richer are all logically consistent.

Solution

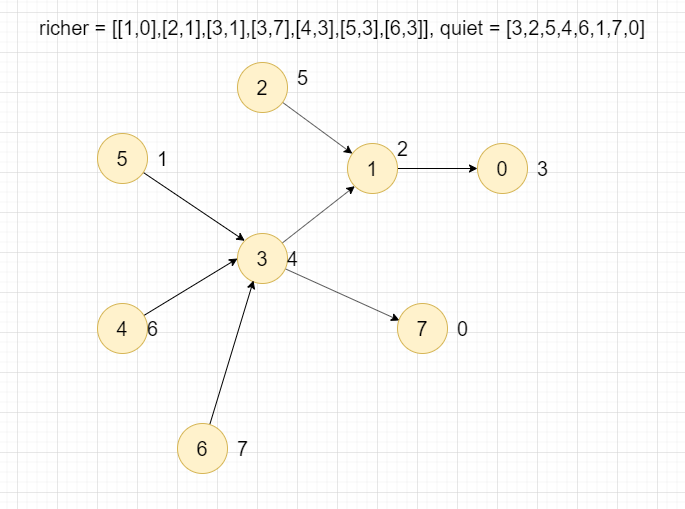
  1. Draw the graph as required
  2. Create a mapping table 【connect】:
    • key: the vertex of the in-degree
    • value: which elements will this vertex of the in-degree point to
  3. Create an in-degree table 【degree】 ：
    • key: the value of the vertex;
      value: how many in-degree elements there are, for example, vertex 3 has 3 in-degree elements (if the vertex is an index, we only need to create an array/list)
  4. Find the key/index that are 0 in the in-degree table, that is, 2, 3, 5, 6, and put these values in the queue
  5. Compare the quiet value of the current popleft value and the quiet value of the outdegree element, and update the element
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# O(n+m) time | O(n+m) space
from collections import deque
class Solution:
    def loudAndRich(self, richer: List[List[int]], quiet: List[int]) -> List[int]:
        n = len(quiet)
        connect = defaultdict(list)
        degree = [0]*n
        queue = deque()
        
        for cur, nxt in richer:
            connect[cur].append(nxt)
            degree[nxt] +=1
        
        for i in range(n):
            if degree[i] == 0:
                queue.append(i)
        
        ans = [i for i in range(n)]
        while queue:
            cur = queue.popleft()
            for nxt in connect[cur]:
                degree[nxt]-=1
                if degree[nxt] == 0:
                    queue.append(nxt)
                
                if quiet[ans[cur]] < quiet[ans[nxt]]:
                    ans[nxt] = ans[cur]
        return ans